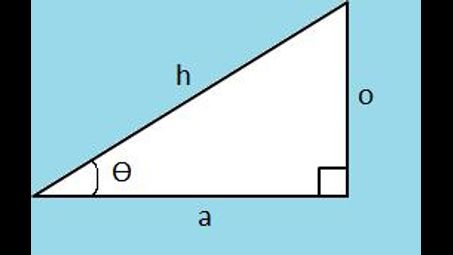
Following the symbols in the image:
Assuming 15cm corresponds to a (the line adjacent to the angle), then you need to use the cosine formula
cos(ø) = a/h
cos(31º) = 15cm/h
h*cos(31º) = (15cm/h) * h
h*cos(31º) = 15cm * 1
h*cos(31º)/cos(31º) = 15cm/cos(31º)
h*1 = 15cm/cos(31º)
h = 16.398
Add your answer:
A right-angled triangle has a hypotenuse of 25cm and one side of 15cm what is the length of the third side?
The length of the third side is 20 cm
What is the missing length of the right triangle which measures 15 cm by 13 cm?
We don't know whether the 15cm happens to be the hypotenuse (longest side) of the right triangle. It makes a big difference. -- If the 15cm is the longest side, then the third side is 7.483 cm. (rounded) -- If the 13cm and the 15cm are the "legs", then the hypotenuse is 19.849 cm. (rounded)
What is the length of the hypotenuse of a right triangle where the two sides are 15cm and 15cm long?
Using Pythagoras' theorem: 15 times the square root of 2 cm in length
What is length ab if cab is 90 degrees and ac is 9cm and bc is 15cm on right angle triangle?
12 cm
How do you find the length of the hypotenuse if the base is 15cm and the height is 8cm?
Use Pythagoras' Theorem : In a right angled triangle the square of the hypotenuse is equal to the sum of the squares of the other two sides. Let H be the hypotenuse then :- H2 = 152 + 82 = 225 + 64 = 289 Then H = √289 = 17cm
A right-angled triangle has a hypotenuse of 25cm and one side of 15cm what is the length of the third side?
The length of the third side is 20 cm
What is the area of a right triangle with sides of 8cm 15cm 17cm?
60 cm2
What is the missing length of the right triangle which measures 15 cm by 13 cm?
We don't know whether the 15cm happens to be the hypotenuse (longest side) of the right triangle. It makes a big difference. -- If the 15cm is the longest side, then the third side is 7.483 cm. (rounded) -- If the 13cm and the 15cm are the "legs", then the hypotenuse is 19.849 cm. (rounded)
What is the length of the hypotenuse of a right triangle where the two sides are 15cm and 15cm long?
Using Pythagoras' theorem: 15 times the square root of 2 cm in length
What is a triangle with sides 11cm 15cm 11cm?
Isosceles
What is length ab if cab is 90 degrees and ac is 9cm and bc is 15cm on right angle triangle?
12 cm
How do you find the length of the hypotenuse if the base is 15cm and the height is 8cm?
Use Pythagoras' Theorem : In a right angled triangle the square of the hypotenuse is equal to the sum of the squares of the other two sides. Let H be the hypotenuse then :- H2 = 152 + 82 = 225 + 64 = 289 Then H = √289 = 17cm
What is the measurement of the third side of a triangle if one side is 15cm and one is 8 cm?
If it's a right angle triangle then by using Pythagoras' theorem the third side is 17 cm
How many triangles have the perimeter of 15cm?
To determine the number of triangles with a perimeter of 15cm, we need to consider the possible side lengths that can form a triangle. The triangle inequality theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. With a perimeter of 15cm, the possible side lengths could be (5cm, 5cm, 5cm) for an equilateral triangle, (6cm, 5cm, 4cm) for an isosceles triangle, or (7cm, 5cm, 3cm) for a scalene triangle. Therefore, there are 3 possible triangles that can have a perimeter of 15cm.
What is the area of a triangle with a base of 10cm and a height of 15cm?
To find the area of a triangle, you use the formula: Area = 1/2 * base * height. Plugging in the values, we get Area = 1/2 * 10cm * 15cm = 75 square cm. Therefore, the area of the triangle with a base of 10cm and a height of 15cm is 75 square cm.
Can you construct a triangle that has side lengths 11cm 12cm and 15cm?
Yes
What is the area of a right triangle with legs of length 9 cm and 12 cm and a hypotenuse of length 15cm?
Area = 1/2*9*12 = 54 square cm
